REVIEW¶
Spectral theorem¶
Course: Math 833 - Modern Discrete Probability (MDP)
Author: Sebastien Roch, Department of Mathematics, University of Wisconsin-Madison
Updated: Nov 20, 2020
Copyright: © 2020 Sebastien Roch
1 Statement and proof of the spectral theorem¶
Theorem (Spectral Theorem): Let $A \in \mathbb{R}^{d \times d}$ be a symmetric matrix, that is, $A^T = A$. Then $A$ has $d$ orthonormal eigenvectors $\mathbf{q}_1, \ldots, \mathbf{q}_d$ with corresponding (not necessarily distinct) real eigenvalues $\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_d$. In matrix form, this is written as the matrix factorization
$$ A = Q \Lambda Q^T = \sum_{i=1}^d \lambda_i \mathbf{q}_i \mathbf{q}_i^T $$where $Q$ has columns $\mathbf{q}_1, \ldots, \mathbf{q}_d$ and $\Lambda = \mathrm{diag}(\lambda_1, \ldots, \lambda_d)$. We refer to this factorization as a spectral decomposition of $A$.
Proof idea (Spectral Theorem): Use a greedy sequence maximizing the quadratic form $\langle \mathbf{v}, A \mathbf{v}\rangle$. How is this quadratic form is related to eigenvalues? Note that, for a unit eigenvector $\mathbf{v}$ with eigenvalue $\lambda$, we have $\langle \mathbf{v}, A \mathbf{v}\rangle = \langle \mathbf{v}, \lambda \mathbf{v}\rangle = \lambda$.
Exercise: Consider the block matrices
$$ \begin{pmatrix} \mathbf{y}\\ \mathbf{z} \end{pmatrix} \quad \text{and} \quad \begin{pmatrix} A & B\\ C & D \end{pmatrix} $$where $\mathbf{y}\in\mathbb{R}^{d_1}$, $\mathbf{z}\in\mathbb{R}^{d_2}$, $A \in \mathbb{R}^{d_1 \times d_1}$, $B \in \mathbb{R}^{d_1 \times d_2}$, $C \in \mathbb{R}^{d_2 \times d_1}$, and $D \in \mathbb{R}^{d_2 \times d_2}$. Show that
$$ \begin{pmatrix} \mathbf{y}\\ \mathbf{z} \end{pmatrix}^T \begin{pmatrix} A & B\\ C & D \end{pmatrix} \begin{pmatrix} \mathbf{y}\\ \mathbf{z} \end{pmatrix} = \mathbf{y}^T A \mathbf{y} + \mathbf{y}^T B \mathbf{z} + \mathbf{z}^T C \mathbf{y} + \mathbf{z}^T D \mathbf{z}. $$$\lhd$
Proof (Spectral Theorem): We proceed by induction.
A first eigenvector: Let $A_1 = A$ and
$$ \mathbf{v}_1 \in \arg\max\{\langle \mathbf{v}, A_1 \mathbf{v}\rangle:\|\mathbf{v}\| = 1\} $$and
$$ \lambda_1 = \max\{\langle \mathbf{v}, A_1 \mathbf{v}\rangle:\|\mathbf{v}\| = 1\}. $$Complete $\mathbf{v}_1$ into an orthonormal basis of $\mathbb{R}^d$, $\mathbf{v}_1$, $\hat{\mathbf{v}}_2, \ldots, \hat{\mathbf{v}}_d$, and form the block matrix
$$ \hat{W}_1 = \begin{pmatrix} \mathbf{v}_1 & \hat{V}_1 \end{pmatrix} $$where the columns of $\hat{V}_1$ are $\hat{\mathbf{v}}_2, \ldots, \hat{\mathbf{v}}_d$. Note that $\hat{W}_1$ is orthogonal by construction.
Getting one step closer to diagonalization: We show next that $W_1$ gets us one step closer to a diagonal matrix by similarity transformation. Note first that
$$ \hat{W}_1^T A_1 \hat{W}_1 = \begin{pmatrix} \lambda_1 & \mathbf{w}_1^T \\ \mathbf{w}_1 & A_2 \end{pmatrix} $$where $\mathbf{w}_1 = \hat{V}_1^T A_1 \mathbf{v}_1$ and $A_2 = \hat{V}_1^T A_1 \hat{V}_1$. The key claim is that $\mathbf{w}_1 = \mathbf{0}$. This follows from a contradiction argument.
Indeed, suppose $\mathbf{w}_1 \neq \mathbf{0}$ and consider the unit vector
$$ \mathbf{z} = \hat{W}_1 \times \frac{1}{\sqrt{1 + \delta^2 \|\mathbf{w}_1\|^2}} \begin{pmatrix} 1 \\ \delta \mathbf{w}_1 \end{pmatrix} $$which, by the exercise above, achieves objective value
$$ \begin{align*} \mathbf{z}^T A_1 \mathbf{z} &= \frac{1}{1 + \delta^2 \|\mathbf{w}_1\|^2} \begin{pmatrix} 1 \\ \delta \mathbf{w}_1 \end{pmatrix}^T \begin{pmatrix} \lambda_1 & \mathbf{w}_1^T \\ \mathbf{w}_1 & A_2 \end{pmatrix} \begin{pmatrix} 1 \\ \delta \mathbf{w}_1 \end{pmatrix}\\ &= \frac{1}{1 + \delta^2 \|\mathbf{w}_1\|^2} \left( \lambda_1 + 2 \delta \|\mathbf{w}_1\|^2 + \delta^2 \mathbf{w}_1^T A_2 \mathbf{w}_1 \right). \end{align*} $$By a Taylor expansion, for $\epsilon \in (0,1)$ small,
$$ \frac{1}{\sqrt{1 + \epsilon^2}} \approx 1 - \epsilon^2/2. $$So, for $\delta$ small,
$$ \begin{align} \mathbf{z}^T A_1 \mathbf{z} &\approx (\lambda_1 + 2 \delta \|\mathbf{w}_1\|^2 + \delta^2 \mathbf{w}_1^T A_2 \mathbf{w}_1) (1 - \delta^2 \|\mathbf{w}_1\|^2/2)\\ &\approx \lambda_1 + 2 \delta \|\mathbf{w}_1\|^2 + C \delta^2\\ &> \lambda_1 \end{align} $$where $C \in \mathbb{R}$ depends on $\mathbf{w}_1$ and $A_2$. That gives the desired contradiction.
So, letting $W_1 = \hat{W}_1$,
$$ W_1^T A_1 W_1 = \begin{pmatrix} \lambda_1 & \mathbf{0} \\ \mathbf{0} & A_2 \end{pmatrix}. $$Finally note that $A_2 = \hat{V}_1^T A_1 \hat{V}_1$ is symmetric
$$ A_2^T = (\hat{V}_1^T A_1 \hat{V}_1)^T = \hat{V}_1^T A_1^T \hat{V}_1 = \hat{V}_1^T A_1 \hat{V}_1 = A_2 $$by the symmetry of $A_1$ itself.
Next step of the induction: Apply the same argument to the symmetric matrix $A_2 \in \mathbb{R}^{(d-1)\times (d-1)}$, let $\hat{W}_2 \in \mathbb{R}^{(d-1)\times (d-1)}$ be the corresponding orthogonal matrix, and define $\lambda_2$ and $A_3$ through the equation
$$ \hat{W}_2^T A_2 \hat{W}_2 = \begin{pmatrix} \lambda_2 & \mathbf{0} \\ \mathbf{0} & A_3 \end{pmatrix}. $$Define the block matrix
$$ W_2 = \begin{pmatrix} 1 & \mathbf{0}\\ \mathbf{0} & \hat{W}_2 \end{pmatrix} $$and observe that
$$ W_2^T W_1^T A_1 W_1 W_2 = W_2^T \begin{pmatrix} \lambda_1 & \mathbf{0} \\ \mathbf{0} & A_2 \end{pmatrix} W_2 = \begin{pmatrix} \lambda_1 & \mathbf{0}\\ \mathbf{0} & \hat{W}_2^T A_2 \hat{W}_2 \end{pmatrix} =\begin{pmatrix} \lambda_1 & 0 & \mathbf{0} \\ 0 & \lambda_2 & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & A_3 \end{pmatrix}. $$Proceeding similarly by induction gives the claim. $\square$
2 Extremal characterization of eigenvalues¶
Definition (Rayleigh Quotient): Let $A \in \mathbb{R}^{d \times d}$ be a symmetric matrix. The Rayleigh quotient is defined as
$$ \mathcal{R}_A(\mathbf{u}) = \frac{\langle \mathbf{u}, A \mathbf{u} \rangle}{\langle \mathbf{u}, \mathbf{u} \rangle} $$which is defined for any $\mathbf{u} \neq \mathbf{0}$ in $\mathbb{R}^{d}$. $\lhd$
Exercise: Let $A \in \mathbb{R}^{d \times d}$ be a symmetric matrix. Let $\mathbf{v}$ be a (not necessarily unit) eigenvector of $A$ with eigenvalue $\lambda$. Show that $\mathcal{R}_A(\mathbf{v}) = \lambda$. $\lhd$
Exercise: Let $\mathcal{U}, \mathcal{V} \subseteq \mathbb{R}^d$ be subspaces such that $\mathrm{dim}(\mathcal{U}) + \mathrm{dim}(\mathcal{V}) > d$. Show there exists a non-zero vector in the intersection $\mathcal{U} \cap \mathcal{V}$. [Hint: Take the union of a basis for $\mathcal{U}$ and a basis for $\mathcal{V}$, then use linear dependence.] $\lhd$
Theorem (Courant-Fischer): Let $A \in \mathbb{R}^{d \times d}$ be a symmetric matrix with spectral decomposition $A = \sum_{i=1}^d \lambda_i \mathbf{v}_i \mathbf{v}_i^T$ where $\lambda_1 \geq \cdots \geq \lambda_d$. For each $k = 1,\ldots,d$, define the subspace
$$ \mathcal{V}_k = \mathrm{span}(\mathbf{v}_1, \ldots, \mathbf{v}_k) \quad\text{and}\quad \mathcal{W}_{d-k+1} = \mathrm{span}(\mathbf{v}_k, \ldots, \mathbf{v}_d). $$Then, for all $k = 1,\ldots,d$,
$$ \lambda_k = \min_{\mathbf{u} \in \mathcal{V}_k} \mathcal{R}_A(\mathbf{u}) = \max_{\mathbf{u} \in \mathcal{W}_{d-k+1}} \mathcal{R}_A(\mathbf{u}). $$Furthermore we have the following min-max formulas, which do not depend on the choice of spectral decomposition, for all $k = 1,\ldots,d$
$$ \lambda_k = \max_{\mathrm{dim}(\mathcal{V}) = k} \min_{\mathbf{u} \in \mathcal{V}} \mathcal{R}_A(\mathbf{u}) = \min_{\mathrm{dim}(\mathcal{W}) = d-k+1} \max_{\mathbf{u} \in \mathcal{W}} \mathcal{R}_A(\mathbf{u}). $$Proof idea: For the local formula, we expand a vector in $\mathcal{V}_k$ into the basis $\mathbf{v}_1,\ldots,\mathbf{v}_k$ and use the fact that $\mathcal{R}_A(\mathbf{v}_i) = \lambda_i$ and that eigenvalues are in non-increasing order. The global formulas then follow from a dimension argument.
Proof: We first prove the local formula, that is, the one involving a specific decomposition.
Local formulas: Since $\mathbf{v}_1, \ldots, \mathbf{v}_k$ form an orthonormal basis of $\mathcal{V}_k$, any nonzero vector $\mathbf{u} \in \mathcal{V}_k$ can be written as $\mathbf{u} = \sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle \mathbf{v}_i$ and it follows that
$$ \langle \mathbf{u}, \mathbf{u} \rangle = \sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle^2 $$$$ \langle \mathbf{u}, A \mathbf{u} \rangle = \left\langle \mathbf{u}, \sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle \lambda_i \mathbf{v}_i \right\rangle = \sum_{i=1}^k \lambda_i \langle \mathbf{u}, \mathbf{v}_i \rangle^2. $$Thus,
$$ \mathcal{R}_A(\mathbf{u}) = \frac{\langle \mathbf{u}, A \mathbf{u} \rangle}{\langle \mathbf{u}, \mathbf{u} \rangle} = \frac{\sum_{i=1}^k \lambda_i \langle \mathbf{u}, \mathbf{v}_i \rangle^2}{\sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle^2} \geq \lambda_k \frac{\sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle^2}{\sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle^2} = \lambda_k $$where we used $\lambda_1 \geq \cdots \geq \lambda_k$ and the fact that $\langle \mathbf{u}, \mathbf{v}_i \rangle^2 \geq 0$. Moreover $\mathcal{R}_A(\mathbf{v}_k) = \lambda_k$. So we have established
$$ \lambda_k = \min_{\mathbf{u} \in \mathcal{V}_k} \mathcal{R}_A(\mathbf{u}). $$The expression in terms of $\mathcal{W}_{d-k+1}$ is proved similarly.
Global formulas: Since $\mathcal{V}_k$ has dimension $k$, it follows from the local formula that
$$ \lambda_k = \min_{\mathbf{u} \in \mathcal{V}_k} \mathcal{R}_A(\mathbf{u}) \leq \max_{\mathrm{dim}(\mathcal{V}) = k} \min_{\mathbf{u} \in \mathcal{V}} \mathcal{R}_A(\mathbf{u}). $$Let $\mathcal{V}$ be any subspace with dimension $k$. Because $\mathcal{W}_{d-k+1}$ has dimension $d - k + 1$, we have that $\dim(\mathcal{V}) + \mathrm{dim}(\mathcal{W}_{d-k+1}) > d$ and there must be non-zero vector $\mathbf{u}_0$ in the intersection $\mathcal{V} \cap \mathcal{W}_{d-k+1}$ by the exercise above.
We then have by the other local formula that
$$ \lambda_k = \max_{\mathbf{u} \in \mathcal{W}_{d-k+1}} \mathcal{R}_A(\mathbf{u}) \geq \mathcal{R}_A(\mathbf{u}_0) \geq \min_{\mathbf{u} \in \mathcal{V}} \mathcal{R}_A(\mathbf{u}). $$Since this inequality holds for any subspace of dimension $k$, we have
$$ \lambda_k \geq \max_{\mathrm{dim}(\mathcal{V}) = k} \min_{\mathbf{u} \in \mathcal{V}} \mathcal{R}_A(\mathbf{u}). $$Combining with inequality in the other direction above gives the claim. The other global formula is proved similarly. $\square$
3 Application to spectral graph theory¶
3.1 Matrices associated to graphs¶
Definition (Adjacency Matrix): Assume the undirected graph $G = (V,E)$ has $n = |V|$ vertices. The adjacency matrix $A$ of $G$ is the $n\times n$ symmetric matrix defined as
$$ \begin{align} A_{xy} = \begin{cases} 1 & \text{if $\{x,y\} \in E$}\\ 0 & \text{o.w.} \end{cases} \end{align} $$$\lhd$
(Source)
$\lhd$
Definition (Incidence Matrix): The incidence matrix of an undirected graph $G = (V, E)$ is the $n \times m$ matrix $B$, where $n = |V|$ and $m =|E|$ are the numbers of vertices and edges respectively, such that $B_{ij} = 1$ if the vertex $i$ and edge $e_j$ are incident and 0 otherwise. $\lhd$
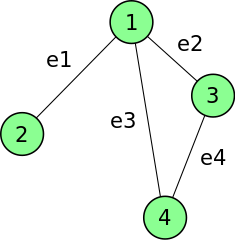
(Source)
$\lhd$
In the digraph case, we have the definitions are adapted as follows. The adjacency matrix $A$ of a digraph $G = (V, E)$ is the matrix defined as
$$ \begin{align} A_{xy} = \begin{cases} 1 & \text{if $(x,y) \in E$}\\ 0 & \text{o.w.} \end{cases} \end{align} $$The oriented incidence matrix of a digraph $G$ with vertices $1,\ldots,n$ and edges $e_1, \ldots, e_m$ is the matrix $B$ such that $B_{ij} = -1$ if egde $e_j$ leaves vertex $i$, $B_{ij} = 1$ if egde $e_j$ enters vertex $i$, and 0 otherwise.
An orientation of an (undirected) graph $G = (V, E)$ is the choice of a direction for each of its edges, turning it into a digraph.
Definition (Oriented Incidence Matrix): An oriented incidence matrix of an (undirected) graph $G = (V, E)$ is the incidence matrix of an orientation of $G$. $\lhd$
g = complete_graph(3)
A = adjacency_matrix(g)
Array(A)
g = smallgraph(:petersen)
A = Array(adjacency_matrix(g))
Array(incidence_matrix(g))
3.2 Laplacian matrix¶
Definition (Laplacian Matrix): Let $G = (V,E)$ be a graph with vertices $V = \{1, \ldots, n\}$ and adjacency matrix $A \in \mathbb{R}^{n \times n}$. Let $D = \mathrm{diag}(\delta(1), \ldots, \delta(n))$ be the degree matrix. The Laplacian matrix associated to $G$ is defined as $L = D - A$. Its entries are
$$ l_{ij} = \begin{cases} \delta(i) & \text{if $i = j$}\\ -1 & \text{if $\{i,j\} \in E$}\\ 0 & \text{o.w.} \end{cases} $$$\lhd$
Observe that the Laplacian matrix $L$ of a graph $G$ is symmetric:
$$ L^T = (D- A)^T = D^T - A^T = D - A $$where we used that both $D$ and $A$ are themselves symmetric. The associated quadratic form is particularly simple and will play an important role.
Lemma (Laplacian Quadratic Form): Let $G = (V, E)$ be a graph with $n = |V|$ vertices. Its Laplacian matrix $L$ is positive semi-definite and furthermore we have the following formula for the Laplacian quadratic form
$$ \mathbf{x}^T L \mathbf{x} = \sum_{e = \{i,j\} \in E} (x_i - x_j)^2 $$for any $\mathbf{x} = (x_1, \ldots, x_n)^T \in \mathbb{R}^n$.
Proof: Let $B$ be an oriented incidence matrix of $G$. We claim that $L = B B^T$. Indeed, for $i \neq j$, entry $(i,j)$ of $B B^T$ is a sum over all edges containing $i$ and $j$ as endvertices, of which there is at most one. When $\{i,j\} \in E$, that entry is $-1$, since one of $i$ or $j$ has a $1$ in the column of $B$ corresponding to $e$ and the other one has a $-1$. For $i = j$, letting $b_{xy}$ be entry $(x,y)$ of $B$,
$$ (B B^T)_{ii} = \sum_{e = \{x, y\} \in E: i \in e} b_{xy}^2 = \delta(i). $$Thus, for any $\mathbf{x}$, we have $(B^T \mathbf{x})_k = x_v - x_u$ if the edge $e_k = \{u, v\}$ is oriented as $(u,v)$ under $B$. That implies
$$ \mathbf{x}^T L \mathbf{x} = \mathbf{x}^T B B^T \mathbf{x} = \|B^T \mathbf{x}\|^2 = \sum_{e = \{i,j\} \in E} (x_i - x_j)^2. $$Since the latter is always nonnegative, it also implies that $L$ is positive semidefinite. $\square$
As a convention, we denote the eigenvalues of a Laplacian matrix $L$ by
$$ 0 \leq \mu_1 \leq \mu_2 \leq \cdots \leq \mu_n. $$Another important observation:
Lemma ($\mu_1 = 0$): Let $G = (V, E)$ be a graph with $n = |V|$ vertices and Laplacian matrix $L$. The constant unit vector
$$ \mathbf{y}_1 = \frac{1}{\sqrt{n}} (1, \ldots, 1)^T $$is an eigenvector of $L$ with eigenvalue $0$.
Proof: Let $B$ be an oriented incidence matrix of $G$ recall that $L = B B^T$. By construction $B^T \mathbf{y}_1 = \mathbf{0}$ since each column of $B$ has exactly one $1$ and one $-1$. So $L \mathbf{y}_1 = B B^T \mathbf{y}_1 = \mathbf{0}$ as claimed. $\square$
By our proof of the Spectral Theorem, the largest eigenvalue $\mu_n$ of the matrix Laplacian $L$ is the solution to the optimization problem
$$ \mu_n = \max\{\langle \mathbf{x}, L \mathbf{x}\rangle:\|\mathbf{x}\| = 1\}. $$Such extremal characterization is useful in order to bound the eigenvalue $\mu_n$, since any choice of $\mathbf{x}$ with $\|\mathbf{x}\| =1$ gives a lower bound through the quantity $\langle \mathbf{x}, L \mathbf{x}\rangle$. That perspective will be key to our application to graph partitioning.
Lemma (Laplacian and Degree): Let $G = (V, E)$ be a graph with maximum degree $\bar{\delta}$. Let $\mu_n$ be the largest eigenvalue of its matrix Laplacian $L$. Then
$$ \mu_n \geq \bar{\delta}+1. $$Proof idea: As explained before the statement of the lemma, it suffices to find a good test unit vector $\mathbf{x}$ to plug into $\langle \mathbf{x}, L \mathbf{x}\rangle$. A clever choice does the trick.
Proof: Let $u \in V$ be a vertex with degree $\bar{\delta}$. Let $\mathbf{z}$ be the vector with entries
$$ z_i = \begin{cases} \bar{\delta} & \text{if $i = u$}\\ -1 & \text{if $\{i,u\} \in E$}\\ 0 & \text{o.w.} \end{cases} $$and let $\mathbf{x}$ be the unit vector $\mathbf{z}/\|\mathbf{z}\|$. By definition of the degree of $u$, $\|\mathbf{z}\|^2 = \bar{\delta}^2 + \bar{\delta}(-1)^2 = \bar{\delta}(\bar{\delta}+1)$.
Using the Laplacian Quadratic Form Lemma,
$$ \langle \mathbf{z}, L \mathbf{z}\rangle = \sum_{e = \{i, j\} \in E} (z_i - z_j)^2 \geq \sum_{i: \{i, u\} \in E} (z_i - z_u)^2 = \sum_{i: \{i, u\} \in E} (-1 - \bar{\delta})^2 = \bar{\delta} (\bar{\delta}+1)^2 $$where we restricted the sum to those edges incident with $u$ and used the fact that all terms in the sum are nonnegative. Finally
$$ \langle \mathbf{x}, L \mathbf{x}\rangle = \left\langle \frac{\mathbf{z}}{\|\mathbf{z}\|}, L \frac{\mathbf{z}}{\|\mathbf{z}\|}\right\rangle = \frac{1}{\|\mathbf{z}\|^2} \langle \mathbf{z}, L \mathbf{z}\rangle = \frac{\bar{\delta} (\bar{\delta}+1)^2}{\bar{\delta}(\bar{\delta}+1)} = \bar{\delta}+1 $$so that
$$ \mu_n = \max\{\langle \mathbf{x}', L \mathbf{x}'\rangle:\|\mathbf{x}'\| = 1\} \geq \langle \mathbf{x}, L \mathbf{x}\rangle = \bar{\delta}+1 $$as claimed. $\square$
Corollary (Extremal Characterization of $\mu_2$): Let $G = (V, E)$ be a graph with $n = |V|$ vertices. Assume the Laplacian $L$ of $G$ has spectral decomposition $L = \sum_{i=1}^n \mu_i \mathbf{y}_i \mathbf{y}_i^T$ with $0 = \mu_1 \leq \mu_2 \leq \cdots \leq \mu_n$ and $\mathbf{y}_1 = \frac{1}{\sqrt{n}}(1,\ldots,1)^T$. Then
$$ \mu_2 = \min\left\{ \frac{\sum_{\{u, v\} \in E} (x_u - x_v)^2}{\sum_{u = 1}^n x_u^2} \,:\, \mathbf{x} = (x_1, \ldots, x_n)^T \neq \mathbf{0}, \sum_{u=1}^n x_u = 0 \right\}. $$One application of this extremal characterization is a graph drawing heuristic. Consider the entries of the second Laplacian eigenvector $\mathbf{y}_2$ normalized to have unit norm. The entries are centered around $0$ by the condition $\sum_{u=1}^n x_{u} = 0$. Because it minimizes the quantity
$$ \frac{\sum_{\{u, v\} \in E} (x_u - x_v)^2}{\sum_{u = 1}^n x_u^2} $$over all centered unit vectors, $\mathbf{y}_2$ tends to assign similar coordinates to adjacent vertices. A similar reasoning applies to the third Laplacian eigenvector, which in addition is orthogonal to the second one.
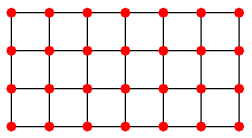
(Source)
g = grid([4,7])
function rand_locs(g)
return rand(nv(g)), rand(nv(g)) # random x and y coord for each vertex
end
(x, y) = rand_locs(g)
hcat(x,y)
gplot(g, layout=rand_locs)
function spec_locs(g)
L = Array(laplacian_matrix(g)) # laplacian L of g
F = eigen(L) # spectral decomposition
v = F.vectors # eigenvectors
return v[:,2], v[:,3] # returns 2nd and 3rd eigenvectors
end
gplot(g, layout=spec_locs)